

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
A body-point as the base model in continuum mechanics
Definition of body-point
Constructing the models of continua with the rotational degrees of freedom, such as the rods, plates, shells and 3D Cosserat continua, body-points are used as the base material objects. A body-point is the material object occupying the zero volume in space. Unlike a point mass, undergoes not only translational but also rotational motions. The body-point is the material object occupying zero volume in space. Position of a body-point is considered to be determined if the position vector R(t) and the rotation tensor P(t) are assigned. In fact, to define the body-point we must specify its kinetic energy.
Definition. The kinetic energy K of a body-point is a quadratic form of its translational and angular velocities:
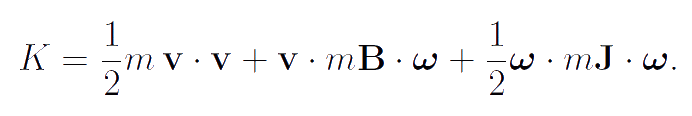 |
Here v is the translational velocity vector, ω is the angular velocity vector, m is the mass of a body-point, mB, mJ are the inertia tensors of a body-point at the actual configuration. It is easy to see that the kinetic energy of a body-point is similar the kinetic energy of rigid bodies. In the rigid body dynamics König's theorem is well-known. This theorem is formulated as follows:
König's theorem. Kinetic energy of a rigid body is equal to the sum of kinetic energy of motion of the center of mass and kinetic energy of rotation about the center of mass.
If we express the kinetic energy of a rigid body using a velocity of any point of the body other than the mass center, we get the formula presented above. In this case, the inertia tensor mB is antisymmetric and completely determined by the radius vector drawn from the mass center to that point of the body, the velocity of which is in the expression for kinetic energy. Thus, a significant difference of body-point from rigid body is that the inertia tensor mB of a body-point can be arbitrary, whereas the inertia tensor mB of a rigid body should be antisymmetric. A mass point and an infinitesimal rigid body are the special cases of body-point. Just these models are traditionally used in continuum mechanics.
A mass point and the infinitesimal rigid body in mechanics of thin-walled structures
In the theories of thin-walled structures with zero bending stiffness, namely in the theories of filaments and membranes, the elementary volume of a continuum is assumed to possess the properties of point mass. The inertial properties of such structures are characterized by the mass density, kinematic is determined by the displacement field, interactions are only forces which associated with the translational motion. In the moment theories describing thin-walled structures with non-zero bending stiffness, such as the rods and shells, the elementary volume of a continuum is considered to be infinitesimal rigid body. Therefore inertia tensors in the moment theories of thin-walled structures have the same structure as the inertia tensors of macroscopic rigid bodies. In some of cases, determining the kinetic energy of an elementary volume, we cannot assume that the radius vector is directed to the mass center, and therefore we cannot apply König's theorem. In these cases we must use the expression for kinetic energy containing tensor B. Examples are given below.
The theory of rectilinear beams and curvilinear rods. In the case of rectilinear beam the mass center of a cross-section is on the middle line. Therefore vector R(s) characterizing the position of the point of rod determines the position of the cross-section mass center. Hence the inertia tensor B is equal to zero. In the case of curvilinear rod the mass center of a cross-section is not located on the middle line (see Figure). Then the inertia tensor B is not equal to zero.

Rectilinear beam and curvilinear rod |
The theory of plates and shells. In the case of plate the mass center of a filament is on the middle plane. Hence B = 0. In the case of shell the mass center of a filament is not located on the middle surface (see Figure). Then B is not equal to zero.
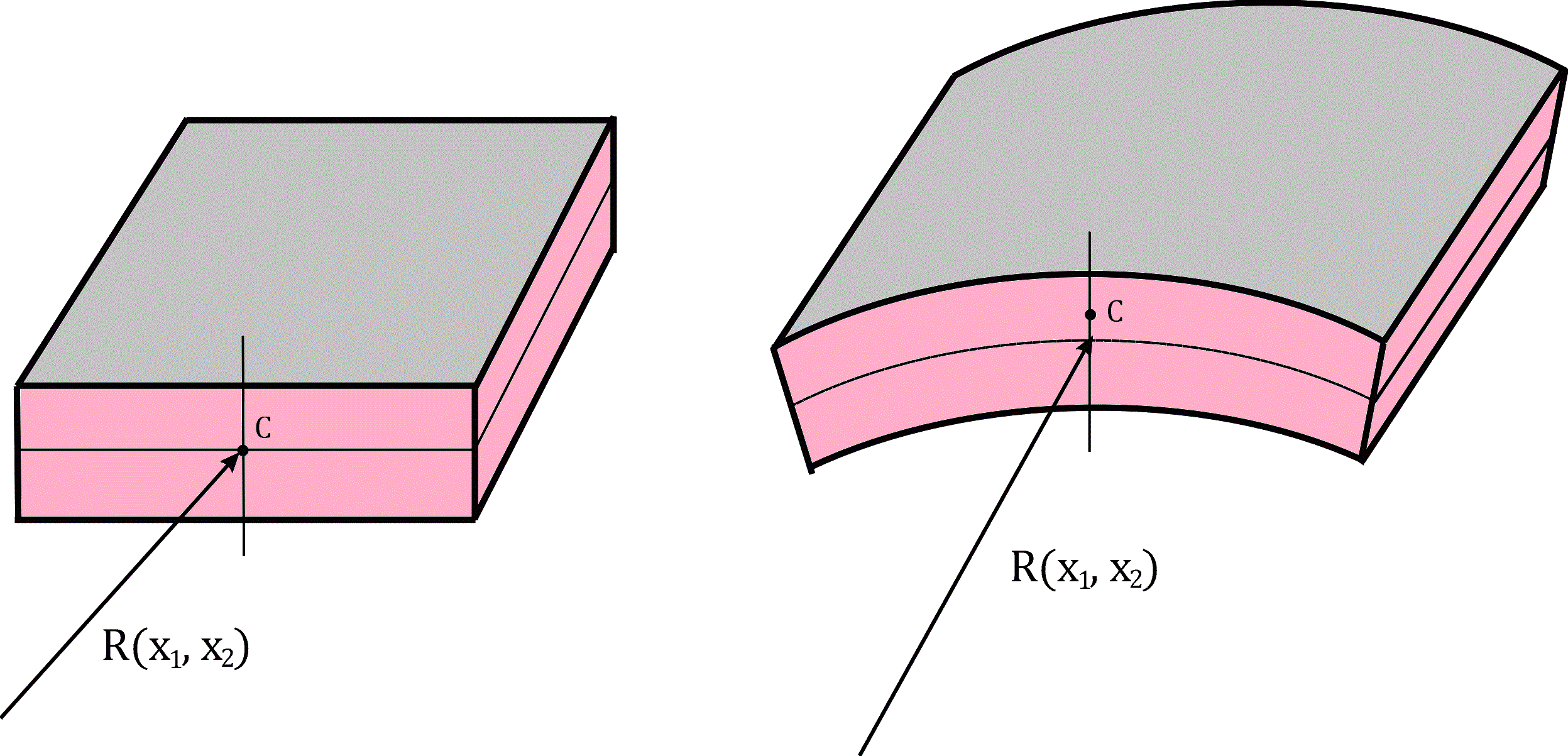
Plate and shell |
At first glance, it seems that carrying curve in a rod and the carrying surface in a shell can be drawn through the centers of mass of elementary volumes. Then the expression for the kinetic energy will be simplified. However, detailed analysis shows that in this case the stiffness tensors will have a more complex structure. Simplification of kinetic energy due to the complexity of the internal energy is unjustified, since it leads to the general complication of the theory. Account of the general theory of curvilinear rods and the theory of shells can be found in books by P.A.Zhilin:
Infinitesimal rigid body in three-dimensional models of continuum mechanics
The classical three-dimensional theories, such as the theory of elasticity, the theory of viscoelasticity based on the models of media with fading memory, the theory of viscoelasticity based on rheological models, and a number of theories of plasticity, are the momentless theories. In the momentless theories the elementary volume of a continuum is similar to the mass point. In 1909 brothers Eugene and Francois Cosserat developed a method for describing three-dimensional continua with rotational degrees of freedom, i.e. such continua the elementary volume of which is the infinitesimal rigid body. For a long time the Cosserat theory found no practical applications. This is due to the fact that in the case of the elastic continuum the corrections associated with the moment interactions are so small that it is impossible to determine experimentally the corresponding modules of elasticity. However, in recent decades the Cosserat continua have been used for describing inelastic continua (in particular, granular continua), for describing continua which possess not only mechanical properties (in particular, ferromagnetics), and also for modelling various physical phenomena and processes and constructing mechanical models of physical fields — see, for example: