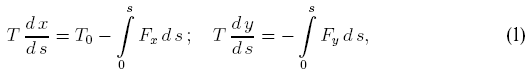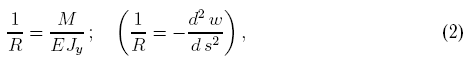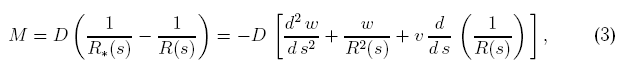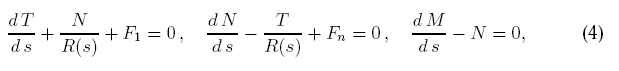Ранний период становления механики сплошной среды

П.А.Жилин Прикладная механика. Основы теории оболочек. СПб: Изд-во СПбГПУ. 2006. 167 с.

Ранний период становления механики сплошной среды

Принято считать, что теория сопротивления твердых тел деформированию основана Галилео Галилеем (1564-1642) в его последнем трактате “Беседы о двух новых науках” (1638). “Беседы” изложены в виде диалогов и разделены на шесть дней. Первые два дня посвящены сцеплению частиц в твердых телах, сопротивлению и разрушению при изгибе и растяжении упругих балок, а также звуковым колебаниям.

Г.Галилей

Здесь формулируются: а) задача о разрушении упругой призмы при изгибе, б) задача о разрушении цилиндрического бруса при продольном разрыве. Первая задача стала отправной для более чем столетнего цикла работ. При рассмотрении второй задачи в рассуждениях Сальвиати (Галилея) неявно присутствуют два фундаментальных понятия: а) принцип затвердевания и б) понятие о напряжении. До Галилея считалось, что сила, потребная для разрыва каната, зависит только от длины каната. Чем длиннее канат - тем меньше сила разрыва. Теперь известно, что из-за наличия дефектов это действительно верно, но в идеальном канате это не так. Требовалась поразительная прозорливость, чтобы, вопреки экспериментальным фактам, утверждать, что сила, потребная для разрыва каната, пропорциональна площади сечения каната и не зависит от его длины.

Принцип затвердевания для теории твердых деформируемых тел в явной форме был сформулирован Гастонов Пардисом (1636-1673) в 1673 году. Он относится к гибким нитям (подвесным мостам, цепным линиям и т.д.) и утверждает, что форма любой выделенной части нити не изменится, если отброшенную часть нити заменить подходящими силами, приложенными к концам выделенной части нити и направленными вдоль касательных к нити в концевых точках. Именно в такой форме принцип затвердевания был использован Якобом Бернулли (1654-1705) в его исследования по гибким нитям. В 1691 г. Я.Бернулли выводит уравнения равновесия гибких нитей при действии произвольной распределенной нагрузки:

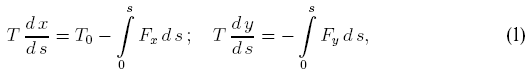где T - продольное усилие; F_x, F_y - внешние погонные усилия; s - длина нити.

Guk (7K)
Р.Гук

Даже в XX веке ничего нельзя добавить к этим уравнениям. В 1660 г. Роберт Гук (1635-1703) открыл (опубликовал в 1676 г.) свой закон упругости. В 1680 г. этот закон был независимо установлен Э. Мариоттом (1620-1684), который применил его к исследованию задачи Г. Галилея об изгибе призмы. В отличие от Галилея, считавшего, что поперечное сечение призмы поворачивается вокруг своего нижнего основания, Мариотт правильно расположил ось вращения, но допустил ошибку при вычислении момента сопротивления. В 1694 г. Я. Бернулли также обратился к решению задачи Галилея и при этом получил следующее уравнение

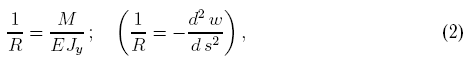где обозначения вполне современны и не нуждаются в пояснениях. Это соотношение принято считать формулой изгиба Бернулли-Эйлера, хотя оно было получено до рождения Л. Эйлера, который, правда, широко использовал его в своих трудах по колебаниям и устойчивости балок.

При выводе (2) Я. Бернулли использовал закон Гука и, кроме того, две гипотезы: “1) сечения, плоские и перпендикулярные к ребрам призмы до ее изгиба, остаются и после изгиба также плоскими и нормальными к этим ребрам и волокнам или продольным элементам, которые становятся криволинейными; 2) волокна, одни растянутые, другие укороченные, сопротивляются независимо, как будто бы они представляли собой малые изолированные призмы, не оказывающие друг на друга никакого действия”.

bbenullija (4K)
Я.Бернулли

Здесь приведена формулировка этих гипотез в трактовке Б.де-Сен-Венана, с.385-386, который считал их ошибочными. В мемуаре Сен-Венан дает формулировку гипотез Я. Бернулли и далее излагает их критику, которая, конечно, является правильной, но только с уровня знаний XIX века. С позиций конца XVII века гипотеза Я. Бернулли вовсе не является гипотезой. Это теоремы, которые легко доказываются при отсутствии напряжений сдвига. Последние еще не были открыты. Поэтому критику “гипотез” Я. Бернулли, по нашему мнению, следовало излагать не как ошибку Я. Бернулли, а как-то иначе. К сожалению, трактовка Сен-Венана попала во многие руководства по теории упругости.

Уравнение (2) сохраняет свое значение и в наши дни, хотя его уже и не называют более уравнением изгиба. Дело в том, что (2) возможно трактовать двояко. Во-первых, можно считать, что момент M в нем задан, тогда по (2) можно найти прогиб балки. Так и поступали Я. Бернулли, Л. Эйлер и другие. Именно в этом смысле (2) и называют уравнением изгиба. Во-вторых, уравнение (2) можно трактовать как определяющее соотношение (аналог закона Гука). Такова современная точка зрения.

Я. Бернулли отчетливо сознавал недостаточность уравнения (2) для создания полной теории изгиба балки и до конца своей жизни не прекращал попыток вывести уравнения равновесия балки при действии поперечной нагрузки.

bbenullii
И.Бернулли

Причем, эти уравнения должны были бы быть вполне аналогичными уравнения (1), т.е. не зависящими от свойств материала балки. Для этой цели Я. Бернулли использовал остроумную модель изгиба балки, сводящую изгиб к продольному растяжению пружины. Попытки Я. Бернулли были неудачны. Причина неудач была установлена значительно позднее Л. Эйлером. Учеником Я. Бернулли был его младший брат Иоганн Бернулли (1667-1748), внесший большой вклад в математику и механику. Однако по интересующему нас вопросу заслуга И. Бернулли была в том, что он воспитал двух великих учеников: своего сына Даниила Бернулли (1700-1784) и Л. Эйлера (1707-1783). В мемуаре, изданном в 1744 году, Л. Эйлер рассматривал балку (здесь же он обобщил уравнение Бернулли (2) на плоский первоначально изогнутый стержень)

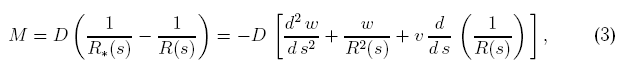где R и R_* — радиусы кривизны стержня до и после деформации; w(s) и v(s) — нормальный и тангенциальный прогибы, как материальную линию, имеющую бесконечно малое поперечное сечение. При этом он считал возможным применять к этой линии все известные законы механики. В этом же мемуаре на с.492-498 Л. Эйлер рассматривает вопрос “Определение абсолютной упругости посредством опытов”. Абсолютной упругостью Л. Эйлер называет жесткость балки на изгиб. Хотя при написании функционала Л. Эйлер считает балку именно линией, в этом пункте он считает, что поперечное сечение балки имеет конечные размеры и устанавливает зависимость жесткости на изгиб от природы материала (модуля упругости Юнга) и размеров поперечного сечения.

Л.Эйлер

Конечный результат Л. Эйлера оказался ошибочным: он повторил ошибку Галилея. Для нас интересен именно способ рассуждений Л. Эйлера, а не конечный результат. Л. Эйлер продолжил труды Я. Бернулли по выводу уравнений равновесия при изгибе балок. При этом ему пришлось сделать два открытия. Первое: необходимость введения перерезывающих усилий (касательных напряжений). Второе: установление независимости уравнений баланса сил и моментов. Именно этих фундаментальных открытий и недоставало Я. Бернулли для вывода уравнений изгиба балки. Строго говоря, понятие напряжений сдвига впервые было введено А. Параном (1666-1716) в 1713 г., но его работа осталась незамеченной и, очевидно, неизвестной Л. Эйлеру, ибо он нигде на нее не ссылается. Здесь следует указать, что Л. Эйлер был первым, кто ввел в употребление ссылки на достижения предшественников. До него такие ссылки носили только негативно-критический характер. Честь второго открытия, одного из самых ярких в творчестве гениального ученого, целиком принадлежит ему. В современных терминах, впрочем, мало отличающихся от использованных Л. Эйлером, эйлеровы законы динамики сформулированы во введении к данной работе. Применительно к системам взаимодействующих материальных точек эти законы могут быть выведены из законов Ньютона, но Эйлер принимает их как независимые постулаты, применимые к любой механической системе. (Это обстоятельство чрезвычайно важно для данной работы). Используя эти законы, Эйлер приходит в 1771 г. 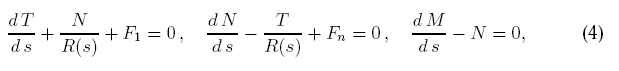к уравнениям равновесия плоского изогнутого стержня formE4

где T, N — растягивающее и пререзывающее усилия; M — изгибающий момент. Кроме уравнений (4) Л. Эйлер предложил обобщение третьего закона Ньютона о равенстве действия и противодействия. В современной записи оно выглядит так

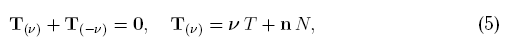где ν и n - векторы единичных касательной и нормали к материальной линии; причем T_ν характеризует воздействие в данном сечении части стержня, находящегося со стороны положительного направления касательной ν на оставшуюся часть стержня. Аналогичное (5) равенство имеет место и для момента M.

Уравнения (4) и (5) сохранились неизменными до наших дней.

Итоги исследованиям по теории стержней подвел Шарль Кулон (1736-1806) в своей небольшой работе, выпущенной в 1773 г.

Kulon
Ш.Кулон

В этой работе Ш. Кулон исправил ошибки своих предшественников и дал правильную формулу для момента сопротивления. Конец XVIII века отмечен двумя, ставшими известными попытками подойти к проблеме построения теории оболочек на основе принципов, использованных в теории стержней. Первая попытка была предпринята Л. Эйлером в 1776 г., когда он предложил рассматривать колокол как совокупность колец, каждое из которых ведет себя как плоский кривой брус. Вторая попытка была совершена Якобом Бернулли--младшим (1759-1789) - сыном Иоганна-П. Бернулли (1710-1790). Он рассматривал (1789) оболочку, “как двойной слой кривых брусьев, причем брусья одной системы пересекаются с брусьями другой системы под прямым углом” с.19. Конечные уравнения, как выяснилось впоследствии, оказались неверными (не было учтено закручивание брусьев).

lagranj
Ж.Лагранж

В 1788 г. выходит первое издание “Аналитической механики” Жозефа-Луи Лагранжа (1736-1813), второе (посмертное) издание вышло, видимо, в 1814 г. Фундаментальным вкладом Ж. Лагранжа в механику является формулировка и систематическое применение принципа возможных перемещений, хотя его частные формулировки появились задолго до Лагранжа. На основе высказанного принципа Лагранж рассматривает и сплошные среды. В частности, в “АМ” впервые выведено уравнение равновесия мембраны. При рассмотрении движения жидкости Ж. Лагранж привел формулировку и дал истолкование линейному тензору деформации

О.Коши

Обычно эту формулу, как указали Л.Г. Лойцянский и А.И. Лурье, приписывают О.Коши, который получил его в 1822 г. Томсон и Тэт показали, что принцип возможных перемещений равносилен при игнорировании притоков энергии немеханического происхождения закону баланса энергии. В.Л. Кирпичев показал, что из него при наложении требования инвариантности относительно группы жестких движений следует Эйлеровы законы динамики. Поэтому трудно согласиться с К. Трусделлом, считающим описанный результат достижением механики второй половины текущего столетия.

Парижская Академия Наук объявила проблему тонких пластинок темой на конкурс 1811 г. В Представленной на конкурс работе Софи Жермен (1776-1831) используется функционал, аналогичный предложенному Д. Бернулли в теории балок. Отличие заключено в замене кривизне стержня суммой главных кривизн изогнутой поверхности пластинки. Как теперь известно, это верно только для защемленной пластины, но на конечном уравнении не сказывается. С. Жермен при выводе уравнения пластины допустила ошибку, которую исправил Ж. Лагранж, рецензировавший ее работу. Уравнение равновесия Ж. Лагранжа-С. Жермен имеет вид

Заканчивая этот параграф, приведем цитату из книги А. Лява, с 20: “Результаты всех трудов и остроумия исследователей в области проблем упругости можно подытожить к к концу 1820 г. следующим образом: несовершенная теория изгиба, ошибочная теория кручения недоказанная теория колебаний стержней и пластинок и определения модулей Юнга”. Далее А. Ляв отмечает большую роль этих исследований в становлении теории упругости. Хотелось бы сформулировать эти итоги несколько иначе. А именно, к 1820 г. были твердо установлены: а) принцип затвердевания, б) Эйлеровы законы динамики с приложением к выводу уравнений равновесия стержней; в) понятие напряжений, особенно в гидромеханике; г) обобщен и многократно применен, в том числе и в сплошной среде, принцип возможных перемещений; д) закон упругости Гука-Мариотта и его приложения к частным задачам; е) общая теория малых деформаций сплошной среды. К сказанному, конечно, следует добавить и те итого, которые сформулированы А. Лявом вслед за приведенной выше цитатой.