

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Interaction of body-point and surrounding medium
Let us discuss the influence of the surrounding medium on a particle imbedded in it. Further we consider two model problems, but we start with some opening remarks. The problem of motion of an oscillator on an elastic waveguide is known. The statement of problem is: a semi-infinite inertial rod is connected with a point mass by means of an inertialess spring; at the initial instant of time the point mass possessed an initial velocity and was removed from the static equilibrium position. It has been proved that the mathematical description of motion of the system consisting of the inertia and elastic elements only can be reduced to the equation of motion of a linear oscillator with viscous damping. The coefficient of damping depends on stiffness of the spring and the quantities characterizing elastic and inertia properties of the rod. The problem of interaction of a body-point with a one-dimensional semi-infinite continuum of body-points and the problem mentioned above are the same except the fact that in the former case the energy dissipates through the rotational degrees of freedom and the equation of motion of an oscillator contains a damping moment instead of a damping force. To prove aforesaid and determine the structure of damping moment we consider two problems being one-dimensional analogue to the problem of the interaction of a body-point with the surrounding medium.
Model problem 1
Now we consider a semi-infinite inertial rod (see Figure) consisting of the body-points of a general kind. The rod is connected with the analogous body-point by means of an inertialless spring working in torsion (rotation about the axis of the rod) only and characterized by the torsional stiffness. The inertia of the body-point is characterized by the mass and the moments of inertia. The inertia of the rod is characterized by the moments of inertia of the cross-section and the linear density of mass. The elastic properties of the rod are characterized by the torsional stiffness. We suppose that the particles of the rod interact only by the moments. The force interaction of the rod particles is assumed to be zero. At the initial instant of time the displacements and the rotation angles as well as the translational and angular velocities of the rod particles are equal to zero. The body-point possesses a non-zero initial angular velocity directed along the axis of the rod and a non-zero initial angle of rotation about the axis of the rod. It is evident that under such initial conditions the system will be in motion which is the longitudinal-torsional oscillations.
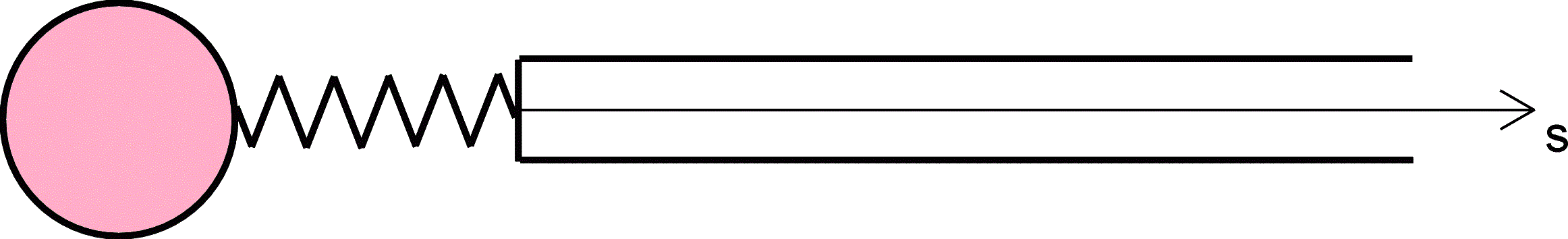 |
It is proved that after elimination of variables characterizing the motion of the rod the problem is reduced to the set of equations:
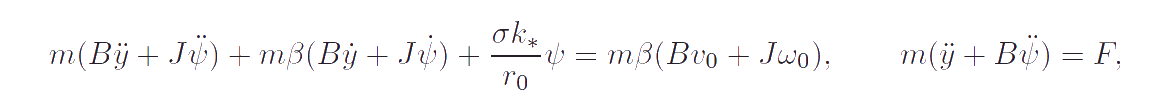 |
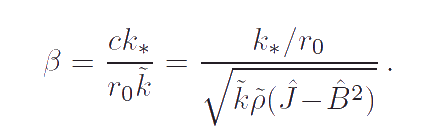 |
According to these equations the moment of viscous damping characterizing the radiation of energy in the surrounding medium is proportional to the angular momentum of the body-point, i. e. it depends on both the angular velocity and the translational velocity. To be exact, the moment of viscous damping is proportional to the difference between the value of angular momentum at the present moment of time and its value at the initial time. On the one hand this means that the moment of viscous damping does not depend on the choice of the inertial reference system. On the other hand, the expression for moment of viscous damping, as well as any constitutive equation, must be independent on the initial conditions. Therefore using the inertial reference system in which the particles of unperturbed rod are motionless we can assume the moment of viscous damping to be proportional to the angular momentum. If the inertial reference system moving relative to the undisturbed rod is used then the expression for the moment of viscous damping should be modified by replacing the absolute velocity of the particle to the particle velocity relative to the undisturbed rod. If B = 0 then the dependence on the translational velocity vanishes. In this case the problem under consideration becomes similar to the problem of the motion of an ordinary oscillator on the elastic waveguide. The coefficient of damping β is expressed in terms of the parameters of the model. Analysis of formula for the coefficient of damping allows us to conclude that increasing the torsional stiffness of the spring connecting the body-point and the rod causes increasing of the radiation in the surrounding medium. A more detailed description of the considered problem can be found in the paper:
Model problem 2
Now we consider the spherical source (see Figure) consisting of the body-points of a general kind. We suppose that the source can pulsate. At the same time the body-points of the spherical source rotate about its radius. The angles of rotation of all body-points are assumed to be the same. The inertia properties of the spherical source are characterized by the mass evenly distributed on the source surface and the moments of inertia. The spherical source interacts with the surrounding medium by means of an elastic connection. The elastic connection constitutes the system of the identical springs working in torsion. Each of them connects the body-point of the spherical source with the body-point of the surrounding medium (see Figure).

Spherical source |
 |
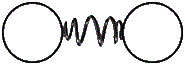
Interaction of particles of the surrounding medium |
It is proved that after elimination of variables characterizing the motion of the surrounding medium the problem is reduced to the set of equations:
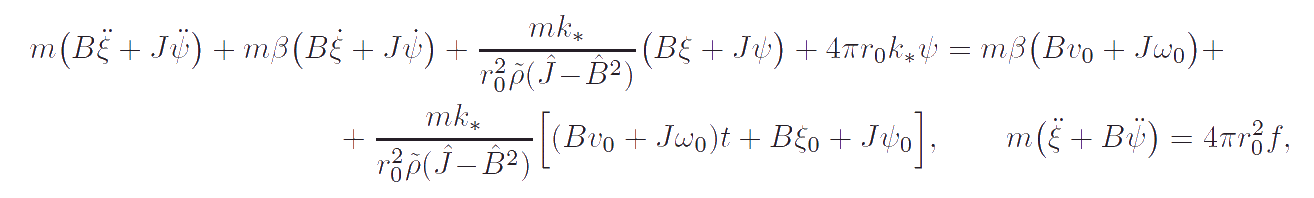 |
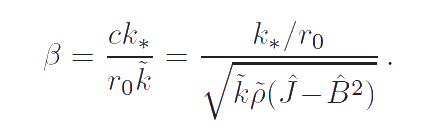 |
These equations, as well as the equations obtained for the case of the interaction of a body-point with the one-dimension continuum, does not depend on the choice of the inertial reference system. A comparison of the equations obtained for two case shows that although these equations somewhat differ from each other nevertheless they have one important similarity. Both of them have the dissipative terms proportional to the angular momentum and the dependence of coefficients of viscous damping β on the parameters of models is the same in both cases. Thus, the analysis of solutions of two model problems gives reason to believe that in the general case the moment of viscous damping characterizing the radiation of energy of a particle into the surrounding medium is proportional to the vector of angular momentum of the particle providing that the inertial reference system fixed relative to the undisturbed surrounding medium is used. A more detailed description of the considered problem can be found in the paper:
Conclusion
The model problems discussed above can provide an explanation of internal damping in material that is caused by the interaction of atoms (or particles constituting atoms) with electromagnetic field and other fields. Certainly, this is not the only kind of internal damping. However, the existence of other mechanisms of internal damping is not a reason to exclude the mechanism described above. The aforementioned model problems can also serve as an explanation of various transport processes (for example, thermal conductivity, electrical conductivity), i.e. any processes described by the diffusion type differential equations. Indeed, if the differential equation has the terms containing the first time derivatives of some physical quantities then these terms can be regarded as "dissipative" terms and their presence in the equation can be interpreted as taking into account the interaction of matter with fields of different nature.
To view PDF files you can download free version of Adobe Acrobat Reader.