Zhilin P.A. Symmetries and Orthogonal Invariants in Oriented Space // Proceedings of XXXII Summer School - Conference “Advanced Problems in Mechanics”. St. Petersburg, Russia. 2005. P. 470-483.

Symmetries and orthogonal invariants

Symmetries and orthogonal invariants are important theoretical tools for many fields of mechanics. Therefore these tools must be applicable to all objects widely used in mechanics. Unfortunately this is not so. The application of the classical theory of symmetry leads to the meaningless results in shell theory and not only in shell theory. The main reason of this is that in many cases we are forced to work in multi-oriented spaces. The classical theory of symmetry and invariants is well defined in non-oriented vector space only. In order to define the cross product of vectors we have to introduce the oriented vector space. There are two different types of tensors acting in oriented space. These tensors are known as polar and axial ones. In oriented space the classical theory of symmetry is well defined for polar tensors. There exist many formally equivalent ways for introduction of the space orientation. In this paper we introduce a definition of the space orientation in such a way that the physical sense of this concept is quiet clear. Besides we restrict ourselves by consideration of the oriented space. In general case this is not enough. For example, in shell theory it is necessary to use multi-oriented space.

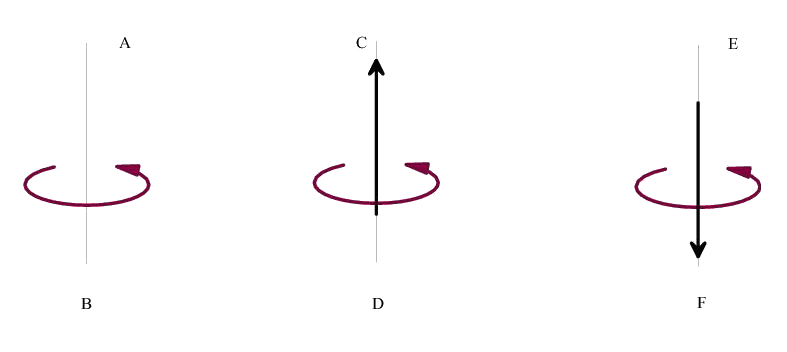
The necessity of orientation of reference system arises due to our desire to take into account the moment interaction in mechanics. In the nature there are two principally different kinds of motion: the translation motion and the spinor (rotational) motion. Under translational motion a body is changing the position in the space. Under spinor motion a body is changing an orientation in the space without changing of position. The changing of translational motion is determined by forces. The changing of spinor motion is determined by moments. Note that in general moments can not be reduced to the concept of the force moment. In order to describe the spinor movements and the moment interactions we must orient the reference system and to introduce some new objects called axial objects in addition to the conventional objects called polar. There are many different but mathematically almost equivalent ways to introduce the space orientation. We prefer a way with clear physical sense. The physical (and mathematical) image of the spinor movement is given by so-called spin-vector whose introduction does not require the space orientation. Let there be given some system of reference (SR). Polar vector is represented in SR as an arrow. In addition to polar vector let us introduce a new object called spin-vector. For this it is necessary to take a strait line in SR called axis of a spin-vector. After that a circular arrow around the axis of a spin-vector must be drown in the plain orthogonal to the axis. Now we have a visual image of the spin-vector — see Figure at the left.
img/inv.gif
The length of the circular arrow is called a modulus of the spin-vector. A direction of a circular arrow shows the direction of a rotation. Spin-vectors describe characteristics of spinor movements. They are convenient for an intuition. However for the formal calculations it is much better to use so-called axial vectors. An axial vector can be obtained from a spin-vector with the help of special rule called an orientation of the reference system. An axial vector a is associated with the spin-vector s by means of the following rule:

1) a is placed on the axis of spin-vector s,
2) modulus of a is equal to the modulus of s,
3) the vector a is directed as shown at the Figure at the center (in such a case we have the right-oriented SR) or as shown at the Figure at the right (in such a case we have the left-oriented SR).

The concept of an axial vector introduced above is the exact expression of a physical idea about angular velocity, moment and so on. The introduction of axial vector does not require any system of coordinates.