

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Phase transitions
Brief overview of existing approaches to the description of phase transitions and structural transformations
The problem of description of phase transitions is a matter that attracts attention of researches working in different areas of science: physics, thermodynamics, nonlinear mechanics. In spite of the difference in approaches and methods, all investigations are based on the opinion that phase transitions are the result of structural modifications of substance under consideration and the nature of interactions at a microlevel. At present time several approaches to mathematical implementation of this concept are developed. Each of them is used to solve certain problems. One of the conventional approaches is based on the assumption of a sharp interface separating different phases. The local interfacial velocity is then calculated from the driving force for the interface motion. The second approach which is based on the theory of mixtures is developed in relation to the description of chemical reactions. The basic assumption of this approach is that there are several constituents at each point of continuum. Depending on various conditions, these constituents can interact or not. The percentage of each constituent is determined by the concentration, which is one of the basic variables. A third approach is based on the diffuse-interface description developed by van der Walls and Cahn. The microstructural evolution is described by the Cahn-Hilliard nonlinear diffusion equation and the time-dependent Ginzburg-Landau equation. This approach is developed primarily in relation to the description of phase transitions associated rather with the change of various physical properties of the substance than with the change of aggregative state. The key point of third approach is the use of so-called order parameters. Sometimes the order parameters really play the role of parameters in the sense that they take one of two values depending on the phase state of the substance. For example, the vector of the electric polarization or magnetization can be order parameters. In some cases, the order parameters are used as independent variables characterizing the process of phase transition. Of course, the above classification is weak in the sense that, for example, the movement of the phase boundary can be described within the framework of both the second and the third approaches, and the concentration of the substance in a mixture can be considered as the order parameter. Nevertheless, the classification seems to be useful because it gives an idea of the differences between the known approaches and allows us to evaluate the place that our approach occupies among other studies.
Liquid–gas phase transition: the van der Walls model
The phase transition problem of liquid–gas is a classical and the simplest one which is presented in the classical textbooks on the equilibrium thermodynamics. The conventional view is that this problem can be solved by using the van der Waals model:
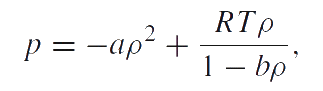 |
Phase diagrams corresponding this equation at different values of temperature are shown in Figure. At T > Tcr the medium can be only in one (gas) state. If T < Tcr three states are possible: two stable states and one unstable. In the critical point K the gas and the liquid phases cannot be distinguished. Their temperature, pressure and density have values, which are characteristic for each phase. Points on the line ac are responsible for the equilibrium of the liquid and the saturated vapor. At low pressure the isotherm presents the properties of the gas. On the left hand side the approximately vertical part of the isotherm is responsible for the very small compressibility of the liquid. The parts ad and ec are responsible for the overheated liquid and the overcooled vapor (metastable state). The part ae is physically not admissible, since here at increasing pressure the volume is also increasing.
|
The van der Waals' model (isotherms near the critical point of the equilibrium) 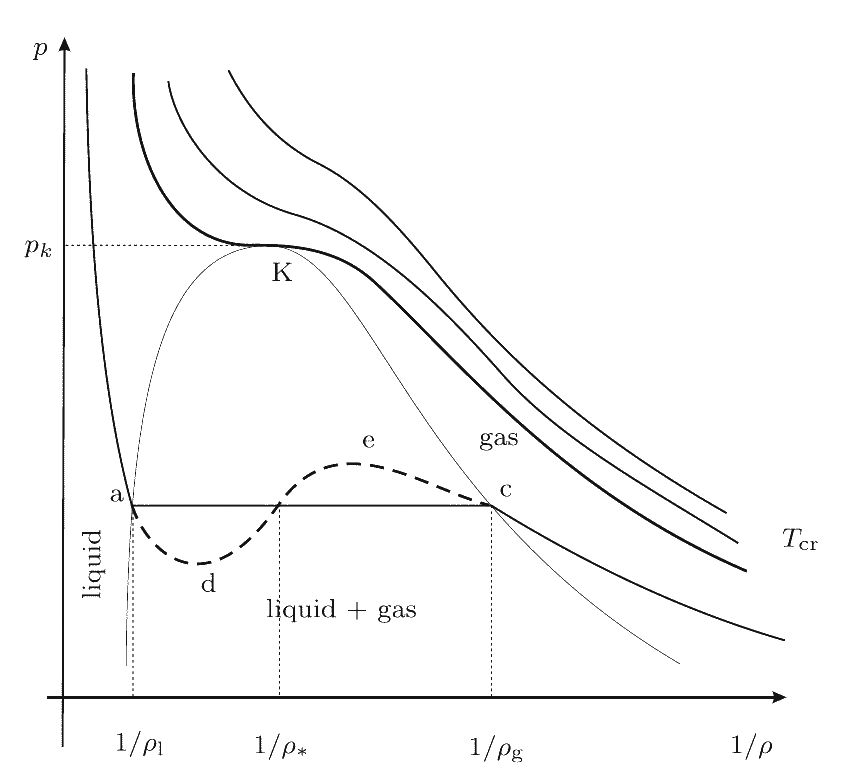 |
It is well known that the critical temperature, pressure and density are related with the parameters of the van der Waals model as follows:
A simple analysis of the van der Waals model results in the conclusion that there are problems which are not discussed in textbooks. For example, for ordinary water
Using these values for critical temperature and pressure we find the parameters of van der Waals' model:
At the end of the section we mention that the van der Waals equation badly describes the behavior of liquids. In particular, the bulk modules of liquids calculated in accordance with the van der Waals equation turn out to be negative.
The aforesaid disadvantages of the van der Waals model are the motivation for the research presented below. The purpose of the investigation is to suggest a model which correctly describes the mechanical and thermodynamic properties of the liquid and the gas and also the process of phase transition. |
The basic idea of the suggested approach
The suggested approach to the description of the liquid–gas phase transition [1] is similar to the methods using the order parameters as independent variables. It is known that the molecules of water and liquids based on water can create clusters that have properties of large molecules. When the temperature increases the clusters begin to disintegrate and the clusters fully disappear when the liquid transforms to a gas. The cluster microstructure model was introduced by various authors. The main idea of our approach to the description of the liquid–gas phase transition is that we consider the matter as a one-component medium which can be either in the liquid state or in the gaseous state. We introduce the additional variable to indicate the number of clusters in a given point of the medium, the value of which allows us to determine whether the substance is a liquid or a gas. In fact, this additional variable can be considered as the order parameter. We suppose that the phase transition should be accompanied by fast changing of the number of particles per unit mass (the ratio of the density of particle distribution to the density of mass) that is due to the fact that at the boiling point the input energy is necessary for the modification of the structure instead of heating.
The mathematical formalization of the suggested approach. To describe structure modifications we introduce the density of the particle distribution as an independent characteristic, and for this quantity we formulate an additional balance equation. Thus, we formulate two independent balance equations, namely the mass balance equation and the particle balance equation:
Here ρ is the mass density; η is the density of particle distribution; χ is the rate of particle production per unit volume. The special choice of the form of the source term χ in the particle balance equation allows us to obtain the desired behavior of this additional variable during the phase transition. The implementation of the approach outlined above is impossible without a clear idea of what is mentioned by a particle in the cluster model of the liquid. There are two possible interpretations. According to one viewpoint the particles are either single molecules or clusters consisting of several molecules. Thus, when the clusters break up, the number of particles increases. Consequently, in a gas the number of particles per unit mass is greater than in a liquid. According to another viewpoint, the particles are molecules and hybridized electron clouds by means of which the molecules are held in clusters. Thus, the cluster consists of several molecules (particles having mass) and several massless particles simulating links between the molecules in the cluster. A system consisting of mass points which are connected by massless springs can be considered as analog of such model of cluster. According to this viewpoint, when the clusters break up, the links disappear, i.e. the number of particles decreases. Hence, in a gas the number of particles per unit mass is smaller than in a liquid. Adoption of one of the viewpoints is a matter of principle, because it has an effect on both the interpretation of the results and the construction of a mathematical model. Therefore, the preference of one point of view is not a question of taste or intuitions. Choosing one or another model it is important to take into account the problems that arise or do not arise in implementation of the mathematical model. We consider the implementation of the two interpretations of the conception "particle" in the cluster model of liquid and we carried out a comparative analysis of two mathematical models.
Comparison of the suggested method with the most famous descriptions of phase transitions
Chemical thermodynamics description of phase transitions is based on the chemical potentials and the chemical affinity of the phase transformation. We use the definition of chemical potential given by P.A.Zhilin. The analysis of various modifications of Zhilin's method and a comparison of Zhilin's method with Truesdell's method can be found in [2], [3], [4]. In accordance with one of Zhilin's method modifications, we suppose that the internal energy is an additive function of the number of particles. Then the equation of energy balance can be reduced to the following local form (in the case of liquins and gases):
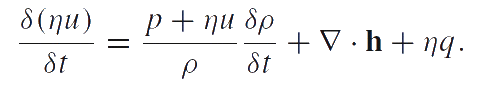
|
Here u is the specific internal energy; q is the energy supply per unit time into the particles of the medium; h is the heat flow. The energy balance equation should be transformed to a special form called reduced equation of energy balance. Let us denote
The quantities T and S defined by this equation are the absolute temperature and entropy related to one particle, respectively. Analogous to the temperature and entropy, η and ψ appear in this equation as conjugate variables. The density of particle distribution η is a measurable quantity. The conjugate variable ψ is supposed to be the chemical potential. The equation given above is the combined equation of structural transitions (e.g. fragmentation) and heat conduction. Thus, the reduced equation of energy balance takes the form:
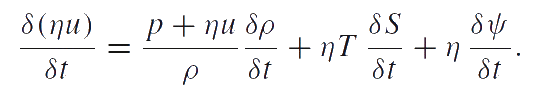
|
Zhilin's definition of chemical potential differs from the classical ones. Use of this this definition allows us to consider the density of particle distribution and the mass density as independent variables. Just due to this fact we can use ratio of the density of particle distribution to the mass density as an order parameter. In addition, we proceed from the supposition that phase transitions are dynamical processes and they can be very quickly ones. That is why the system of basic equations of the suggested model includes the equations of motion. As a result the suggested approach allows us to describe essentially non-equilibrium processes. In contrast to this approach in chemical thermodynamics quasi-equilibrium processes are considered since the method of description of evaporation and condensation processes is based on the Clausius-Clapeyron equation which describes the sequence transitions from one equilibrium state to another.
In continuum mechanics there are different approaches to the description of the thermodynamic processes:
Almost all known models of continuum mechanics describe the situation when the number of particles in the medium does not vary. That means the linear dependence between the density of particle distribution and the density of mass. In this case the density of particle distribution is excluded and all quantities are considered to be additive functions of mass. We consider the density of particle distribution and the density of mass as independent variables and we assume the internal energy and the entropy to be additive functions of number of particles, i.e. that variable which is associated with the order parameter. This circumstance and the fact that the ideas of methods based on the use of order parameters are combined with the methods of continuum mechanics and applied to the description of phase transitions associated rather with the change of aggregative state of matter than with change of its certain physical characteristics distinguish our method from the known approaches. Our approach allows us to describe both phase states with different mechanical and thermodynamic parameters in a framework of a unified model. At the same time our approach allows us to describe the behavior of matter immediately during the phase transition.
Publications
To view PDF files you can download free version of Adobe Acrobat Reader.