

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Alternative models of thermal conductivity and internal damping
In continuum mechanics the temperature is considered to be a quantity measured by thermometer and any mechanical interpretation of temperature is left out. In kinetic theory and statistical physics the temperature is considered as average kinetic energy of the chaotic motion of molecules. The conception of thermal motion of molecules does not contradict continuum mechanics. However, this mechanical model of temperature can not be used to derive the equations of continuum mechanics since the chaotic motion of molecules is ignored in continuum mechanics and the temperature is connected with the internal energy. Our purpose is to suggest the mechanical interpretation of the temperature which can be foundation for description of thermal processes within the framework of continuum mechanics and by using the methods of continuum mechanics. The main idea is to introduce a continuum with internal structure and additional degrees of freedom. We believe that characteristics of motions and interactions connected with internal structure can be associated with the temperature and other thermodynamical quantities. A new approach to derivation of the theory of thermoviscoelasticity is suggested. Neither the hypothesis of fading memory nor the rheological models are used within the framework of this approach. The approach is based on the mechanical model of a one-rotor gyrostat continuum. In special cases the mathematical description of this model is proved to reduce to the equations of the coupled problem of thermoelasticity, the self-diffusion equation and the equation describing the flow of viscous incompressible fluid. In the context of this model we consider the original treatment of physical nature of the mechanism of thermal conduction and internal damping. On the base of the suggested theory we obtain the dependence of the acoustic wave attenuation factor on a signal frequency. This dependence is in close agreement with the classical dependence in the low-frequency range and agrees with the dependence obtained on the base of the phonon theory in the hypersonic-frequency range. We discuss some ways of determination of the volume and shear viscosities and the heat flow relaxation time scale by using known values of the sound velocity and the acoustic wave attenuation factor. The obtained values of the heat flow relaxation time scale are compared with the values derived from the phonon theory.
 |
 |
 |
 |
Description of mechanism of thermal conductivity and internal damping by means of two component Cosserat continuum
The physical object under consideration is a conventional isotropic homogeneous material without microstructure, inclusions, etc. This material has elastic, viscous and thermodynamic properties. In order to describe the thermodynamic processes in the material by means of a mechanical model without using statistical methods we introduce the continuum possessing internal rotational degrees of freedom (see [2], [3], [4], [5], [8]). The internal degrees of freedom are used for modeling the thermal processes. Motions associated with the internal degrees of freedom have no relation to the real motions of the material particles. Characteristics of the motions associated with the internal degrees of freedom as well as characteristics of the interactions associated with the internal degrees of freedom should be considered as analogs of thermodynamic quantities. The main ideas of the suggested theory consist in the following:
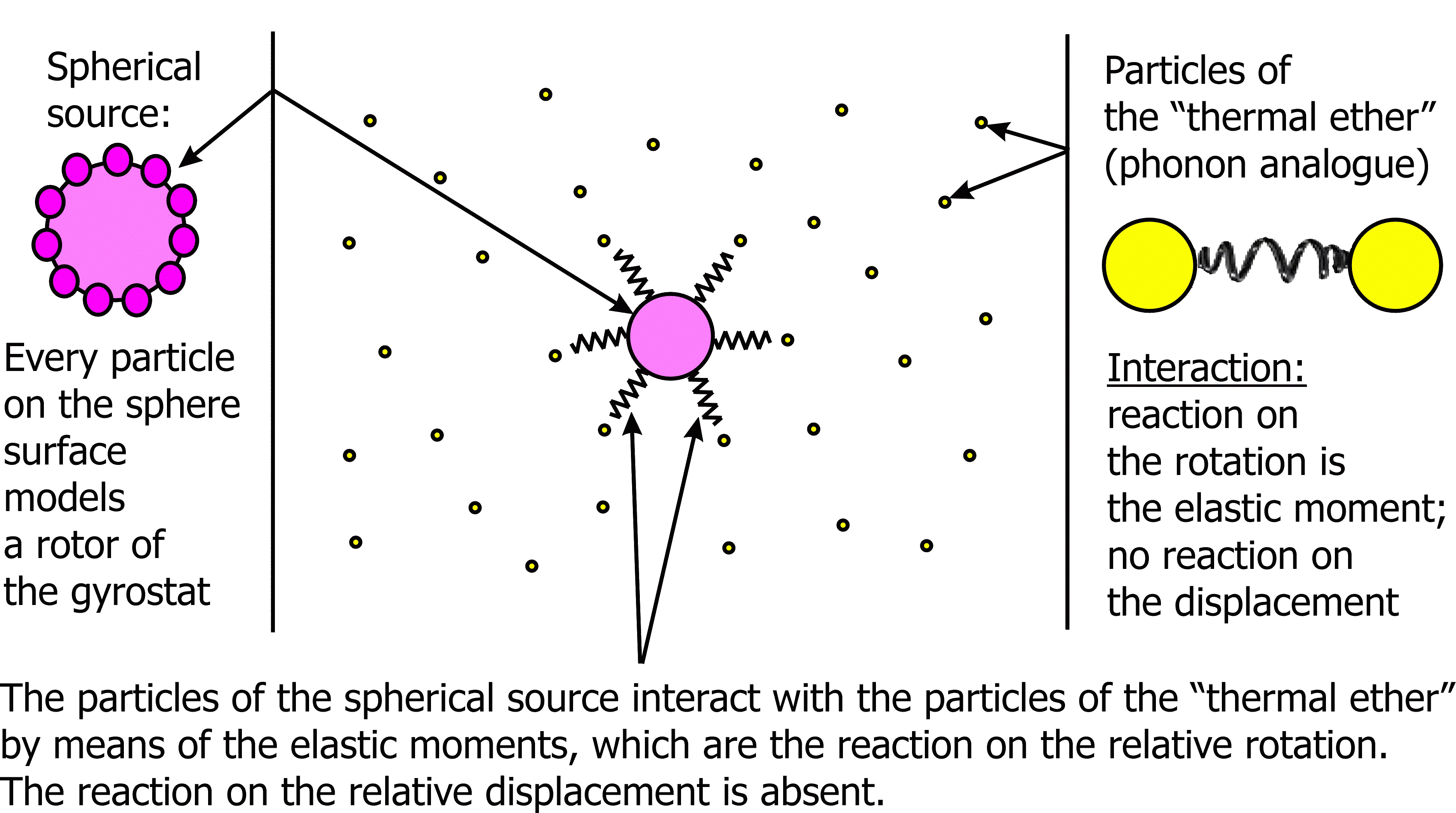
For modeling a material medium we use the one-rotor gyrostat continuum. The one-rotor gyrostat is a complex object which consists of the carrier body and the rotor (see Figure). The rotor can rotate independently of rotation of the carrier body, but it can not translate relative to the carrier body. To explain the physical meaning of the suggested model we give the following arguments. For modeling media with a combination of various physical properties we suggest to consider atoms as complex particles with internal rotational degrees of freedom (see [3], [8]). Number of rotors inside the particles depends on the number of physical properties of the substance that should be taken into account. If only one non-mechanical property of the substance, in the case in question the ability to heat conduction, should be taken into account then one internal rotor is enough. Since the classical theory of thermoelasticity is momentless theory, at first sight it seems that the one-rotor gyrostats continuum is too complicated model, and it can be replaced by the Cosserat continuum. However, our purpose is to suggest a mechanical model of thermal processes which can be used for any continuum models including the cases when describing the mechanical processes is important to take into account the moment interactions. The thermoelastic shell is an example of such a model (see [6]). Since we use a continuum description, it is necessary to clarify the relationship between the continuous and discrete kinematic characteristics of the medium. The position vector of some point of continuum determines position of the mass center of a representative volume which contains billions of atoms. The continuous characteristics of rotational motions are the quantities averaged over all atoms in the representative volume.
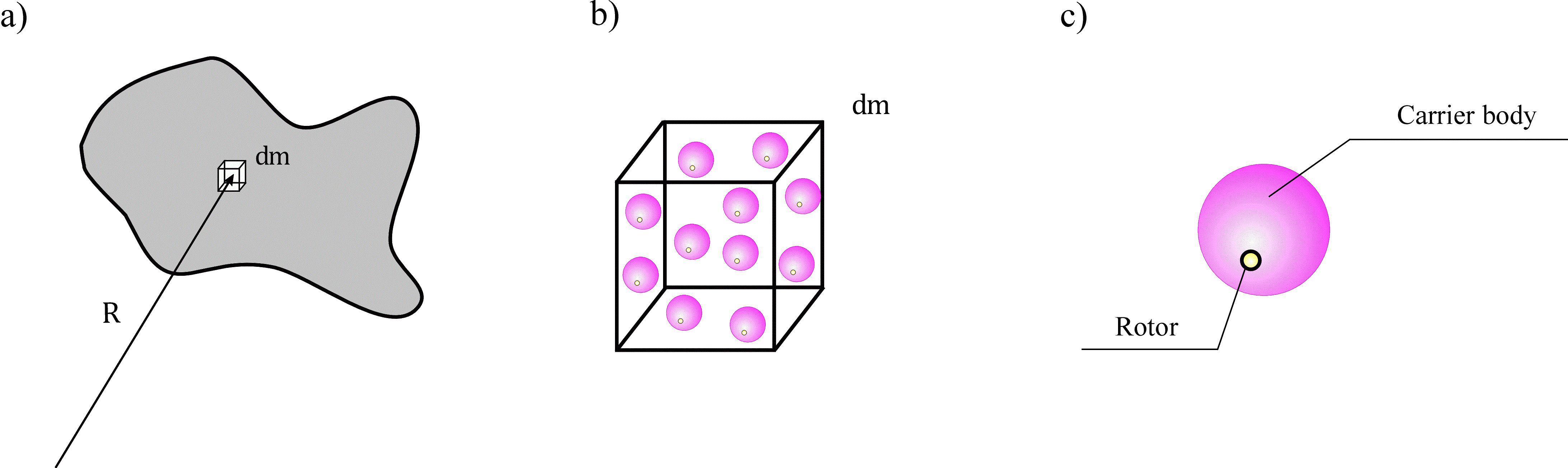
Model of material with elastic, viscous and thermodynamic properties: a) a representative volume in continuum; b) the representative volume on a large scale; c) one-rotor gyrostat. |
Analogy between the mechanical characteristics associated with the rotors and the thermodynamic quantities. The one-rotor gyrostat continuum is considered to be elastic. The interaction of carrier bodies of the gyrostats is charged with the mechanical processes. The interaction of rotors models the thermal processes. The interference of carrier bodies and rotors provides the interplay of mechanical and thermal processes. In our model the spherical part of moment stress tensor characterizing the interaction of rotors is analogue of the absolute temperature. The corresponding angular deformation is analogue of the entropy density (the entropy per unit volume). Dimensions of the temperature and the entropy introduced in the framework of our model are different from those in classical thermodynamics. This problem can be solved by introduction of a normalization factor. Following the above-mentioned mechanical interpretation of temperature and entropy we derive the heat conduction equation from the angular momentum balance equation for the rotors. Due to the presence of inertial terms in the angular momentum balance equation we obtain the heat conduction equation of hyperbolic type. Particles of the material medium are considered to be embedded into some medium having infinite extent. This medium represents the "physical vacuum", the "field", the "ether", or something like that. In what follows it will be called the "thermal ether". A two-component medium is presented in Figure. One component of this medium is a continuum of one-rotor gyrostats and other component is a continuum called the "thermal ether". We are not going to study the interaction of media constituting the two-component continuum. We consider the gyrostats continuum as an object under study. The "thermal ether" positioned in space between gyrostats is an external factor with respect to continuum under study. We model the influence of the "thermal ether" on the gyrostats by an external moment in the equation of the rotors motion. Structure of this moment is chosen based on the analysis of the model problems (see [4], [5], [8]). When the heat conduction equation is derived from the angular momentum balance equation for the rotors it is the presence of the aforesaid external moment that in this balance equation that causes the appearance of the first time derivatives in the heat conduction equation.
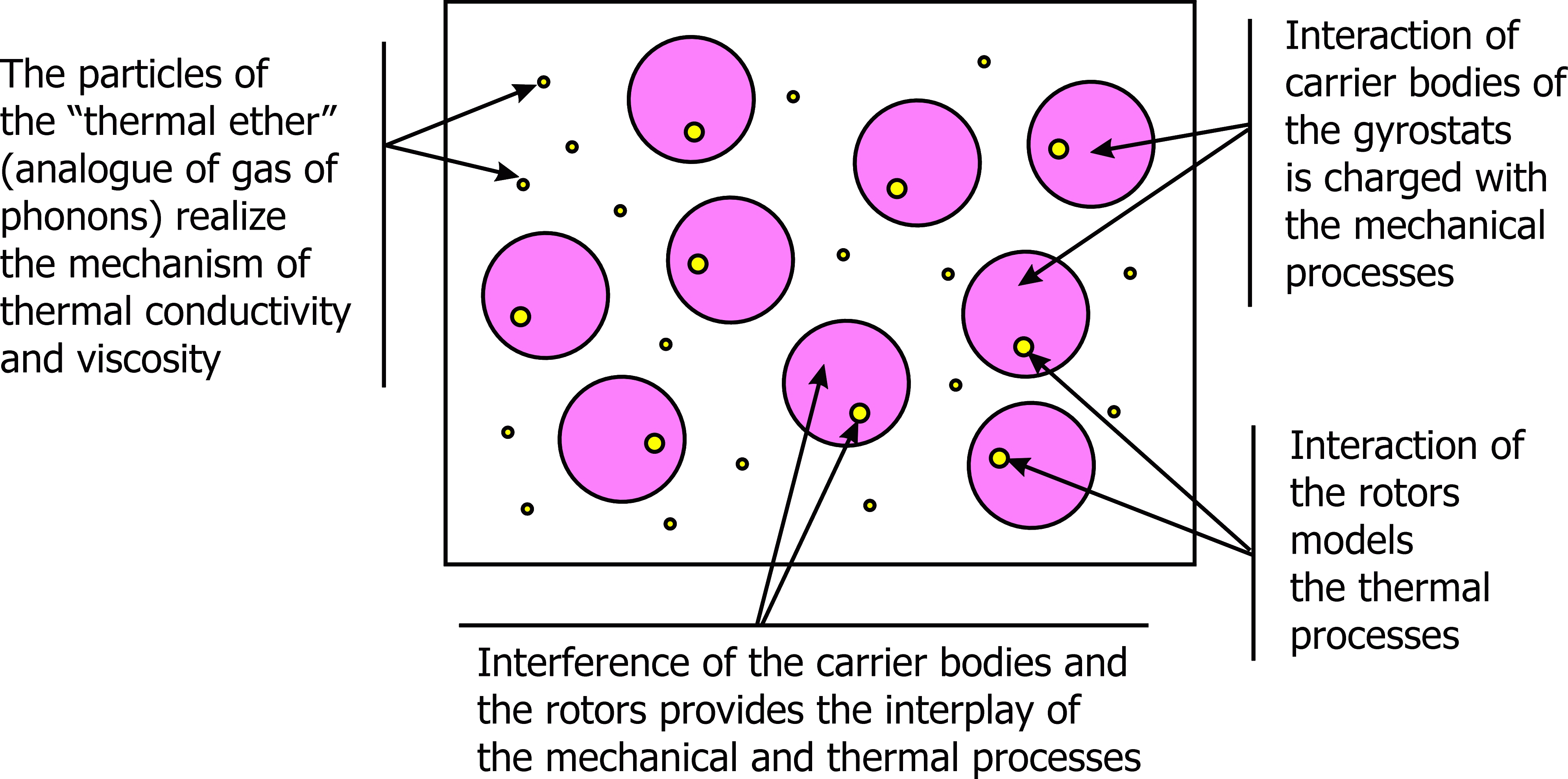 |
When modeling a thermoelastic medium by means of the one-rotor gyrostats continuum, this continuum is considered to be a chiral medium. In view of the foregoing analogy between mechanical and thermodynamical quantities the temperature and entropy are the axial scalars (pseudoscalars) whereas in the classical theory they are the polar scalars. As a consequence, there is one problem. According to the theory of symmetry if the temperature and entropy are considered to be polar scalars then in the case of a conventional isotropic medium the tensor describing the thermal expansion must be the spherical part of tensor. If the temperature and entropy are considered to be axial scalars then, in accordance with the theory of symmetry, the tensor characterizing the thermal expansion is equal to zero. Therefore, if we consider a medium consisting of gyrostats to be isotropic in the conventional sense, then there is a contradiction with the experimental facts. Of course, this is unacceptable. The solution is as follows. We assume that the medium is chiral, at least in respect of the microstructure. A chiral medium is the medium whose local properties are not invariant under mirror reflections. Thus, the symmetry group of a chiral isotropic medium contains the rotation tensors by an arbitrary angle about an arbitrary axis and does not include any mirror reflection tensors. As a rule, the chirality of medium is caused by the chirality of elements constituting this medium. Usually, chiral media are anisotropic. However, there are isotropic chiral media. These are the media consisting of chiral particles. To substantiate the hypothesis that the continuum of one-rotor gyrostats simulating the thermoelastic medium can be considered as a chiral medium, we suggest the following arguments. Let us assume that gyrostats simulate atoms. Then the microstructure of the gyrostat continuum reflects (in the integral sense) some properties of the internal structure of atoms. In this case, the hypothesis of the chirality of the medium with respect to the microstructure does not seem strange. Indeed, the atoms consist of elementary particles which have the spins, i.e. they are the gyrotropic, or what is the same, the chiral objects. Moreover, it is well known, for example, that there exist optically active media which behave as chiral media in relation to electromagnetic waves and do not exhibit the properties of chirality with respect to mechanical effects. The considered medium possesses the similar properties. It behaves as a chiral medium with respect to thermal processes and as an ordinary isotropic medium with respect to purely mechanical process. If the temperature and entropy are considered to be axial scalars, then in the case of a chiral isotropic medium the tensor characterizing the thermal expansion is the spherical part of tensor (see [6]) that is in full agreement with the experimental data.
 |  | 
|
Mechanism of thermal radiation. Numerous experiments show that, for example, diatomic molecules have spectra lying in far infrared area (so-called rotational molecular spectra). These spectra consist of infinite series of approximately equidistant lines. Usually, such spectra are considered as a rotational ones due to the quantum mechanical model explaining the presence of these spectra. The existence of infinite spectra shows that molecules can not be considered as systems with finite number of degrees of freedom. For example, a diatomic molecule can not be a system with 12 degrees of freedom only, as in the case with a system of two rigid bodies. This seems like a contradiction, since it is widely accepted that molecules are systems of atoms, i.e. systems with finite number of degrees of freedom. As a rule, the contradiction is used as an argument that such systems can be described only by means of a using quantum-mechanical approach. Indeed, in the frames of quantum mechanics, the infinite spectrum can be described as a consequence of rotational energy quantization. We show that the contradiction can be eliminated within the framework of classical mechanics, assuming that interaction between atoms in a molecule is not instantaneous, i.e. it is not described by a potential, which depends only on position and orientation of the atoms in a molecule. We assume that the interaction of atoms in molecules are determined by some partial differential equations which can be treated as the equations describing the "thermal ether". In fact, we model molecules by discrete-continuous systems, which are known to have infinite spectra. Thus, our approach based on the concept of the "thermal ether" allows us to describe molecular spectra in the infrared spectral area within the framework of classical mechanics (see [1]). A good agreement of theoretical results with experimental data measured in far infrared spectral area is achieved (see the Tables).
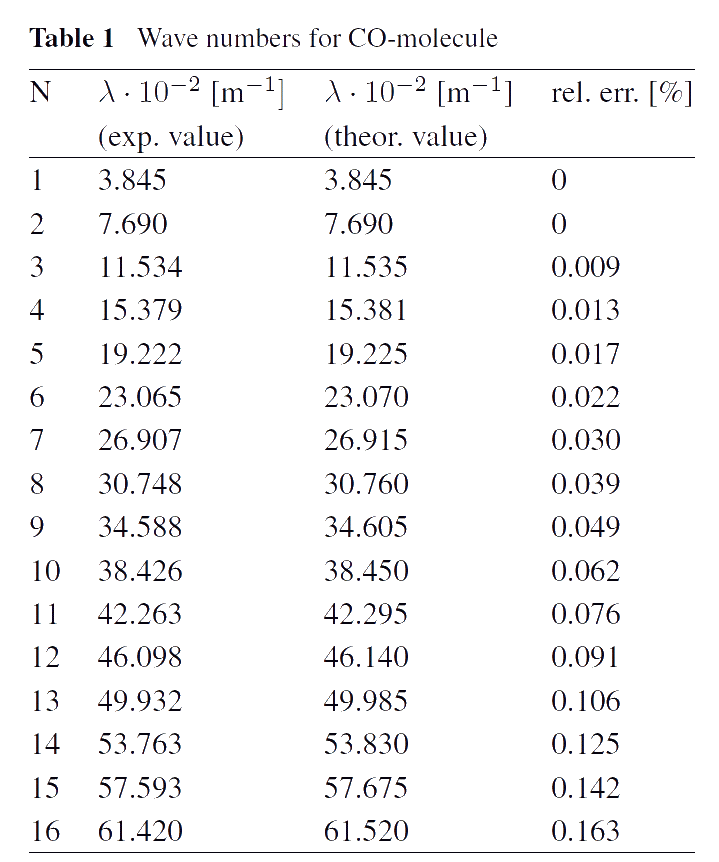 |
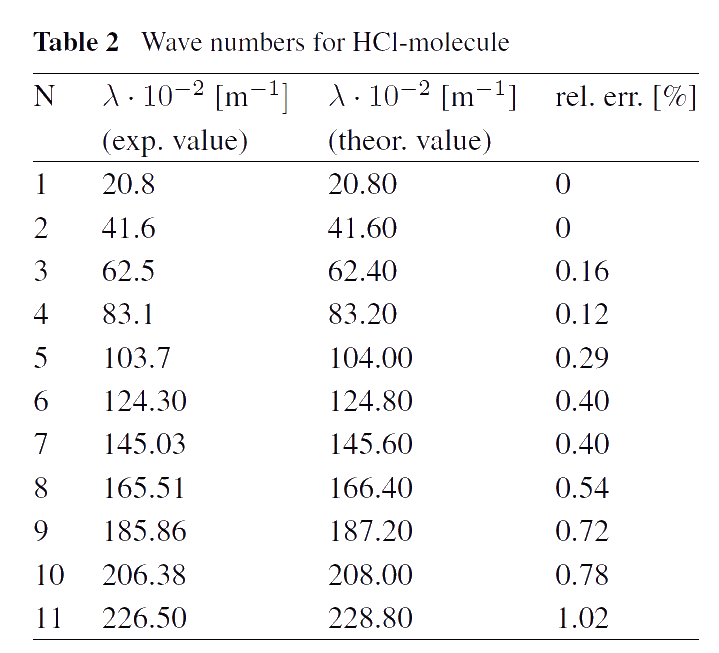 |
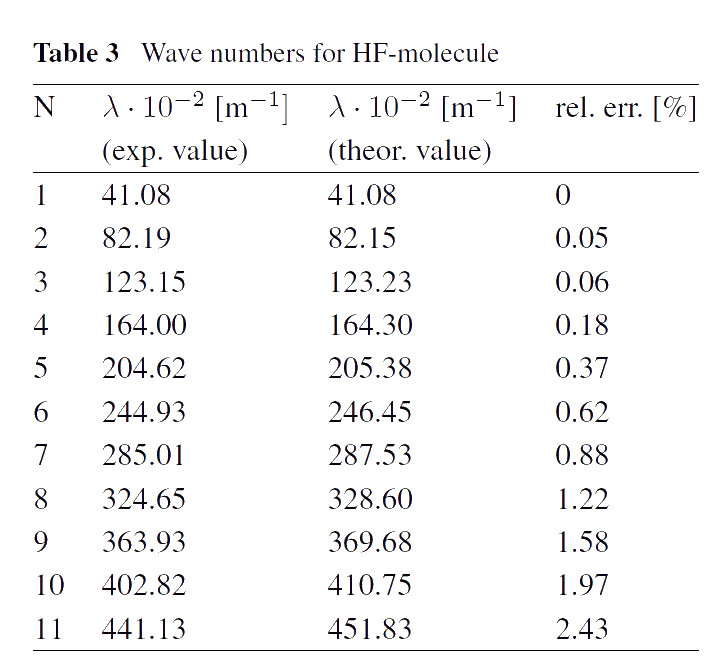 |
Mechanism of thermal conductivity and internal damping. The rotors of gyrostats interact with the "thermal ether" by means of elastic moments concerned with the rotational degrees of freedom. We suppose the heat conduction mechanism to be provided just due to the interaction between the rotors and the "thermal ether". The motion of the rotors of gyrostats cause the appearance of waves in the "thermal ether". As a result the certain part of energy of the material particles is transmitted to the neighboring material particles, and some of the energy is dissipated (is spent on the formation of waves and carried away by these waves). We suppose the internal damping mechanism to be provided due to the energy dissipation into the "thermal ether". This is similar to that on moving a rigid body in a liquid the energy losses are caused by three factors: 1) the friction between the rigid body and liquid; 2) the formation of vortices in the liquid; 3) the formation of waves in the liquid, and the greatest loss of energy is related to formation of waves. The difference is the fact that the interaction of material particles with the "thermal ether" occurs over the rotational degrees of freedom whereas the interaction of a rigid body with a liquid occurs over the translational degrees of freedom. Certainly, we do not rule out the existence of other internal damping mechanisms (in particular, that are considered in the classical books on viscoelasticity). We develop an original method for describing the internal damping. Our model allows us to describe the internal damping inherent to even the materials that are usually considered to be non-viscous, for example, the ideal crystals. So we believe that the mechanism of internal damping inherent in our model has a physical nature different from the physical nature of internal damping modeled by the traditional methods. We show that due to the aforesaid mechanism the attenuation of acoustic waves takes place and some part of mechanical energy is transformed into heat — see [8]. Based on these facts we can assert that we describe some kind of internal damping.
 |
For modeling rotors of gyrostats and particles of the "thermal ether" we use the body-points of a special kind. The carrier bodies of gyrostats are classical body-points whose inertial properties are analogous to that of a rigid body. The rotors of gyrostats, as well as the particles of the "thermal ether", are the body-points of a special kind. The kinetic energy K, momentum K1 and proper angular momentum K2 of these body-points have the form:
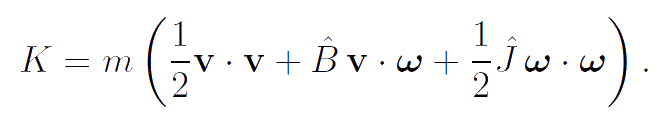 |
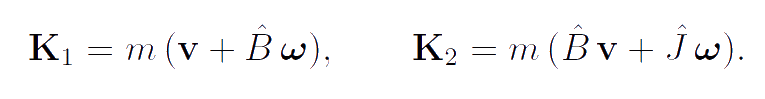 |
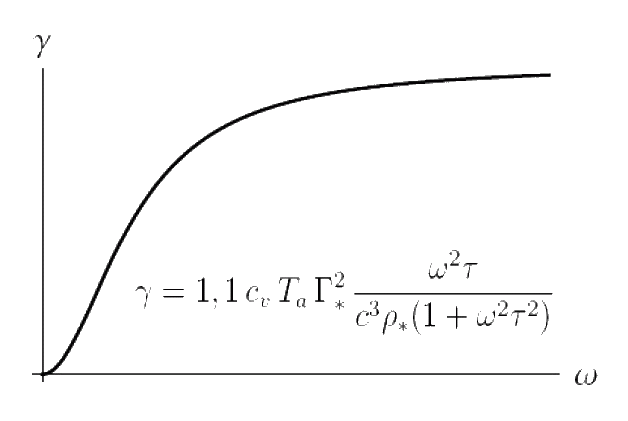
The body-points used for modeling rotors of gyrostats and the particles of the "thermal ether" have the inertia tensors which are the spherical part of tensors. It is important to note that such body-points differ from the infinitesimal rigid bodies by the additional parameter B which characterizes the symmetric part of the corresponding tensor of inertia. In the case of infinitesimal rigid body this parameter equals to zero since the corresponding tensor of inertia is antisymmetric one. The considered body-points of a special kind possess the property of dynamic relatedness of translational and rotational motions — see [4]. The use of these body-points provides additional opportunities to account for the mutual influence of mechanical and thermodynamical processes. Now we argue that statement. According to the quantum-mechanical ideas in solid bodies the dependence of the acoustical absorption factor γ on the frequency ω is as follows. In the range of relatively low frequencies γ is proportional to ω2 (Akhiezer mechanism of absorption), at frequencies of 1010—1011 Hz the acoustical absorption factor γ is proportional to ω (Landau–Rumer mechanism of absorption), and at higher frequencies γ tends to a constant. According to the classical theory of thermoelasticity the acoustical absorption factor γ is proportional to ω2 at all frequencies. The dependence of γ on the frequency obtained by using of the hyperbolic type theory of thermoelasticity is in qualitative agreement with the quantum-mechanical concepts. (Note that the hyperbolic type theory of thermoelasticity contains one additional parameter compared with the classical theory of thermoelasticity — see [7]. This parameter is called the relaxation time of the heat flow.) Neither the classical nor the hyperbolic type theory of thermoelasticity allow us to achieve quantitative agreement between theoretical and experimental values of γ. The suggested theory of thermoviscoelastisity, as well as the hyperbolic type theory of thermoelasticity, is in qualitative agreement with the dependence given by the quantum-mechanical theory (see [8]). Furthermore, the suggested theory contains the additional parameters including the parameter B which can be chosen so that the theoretical values of the acoustical absorption factor and the absorption factor of transverse waves will be in quantitative agreement with the their experimental values (see [8]).
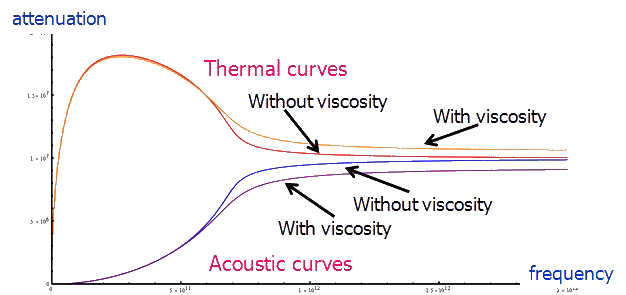
The suggested theory of thermoviscoelasticity |
Quantum mechanical approach |
Conclusion. To describe thermal processes, we suggest an original mechanical model which is an alternative to the mechanical model adopted in the kinetic theory and statistical physics. A mathematical description of this model is developed in the framework of the linear theory. In the future, we intend to carry out further development of the theory in two directions. The first one is concerned with consideration of nonlinear effects in the context of the same mechanical model. This is necessary for describing the behavior of substances in the states near the phase changes and heat-conduction processes under the circumstances of quickly varying and super-high temperatures. The second direction is related to modification of the mechanical model by taking into account the additional degrees of freedom for introducing the chemical potential and a number of additional physical characteristics of the medium. This is necessary to describe the phase changes and chemical reactions and also to account for the interaction of the substance with the electromagnetic field and to describe the thermoelectric and thermomagnetic effects.
Publications
To view PDF files you can download free version of Adobe Acrobat Reader.